在高处向下望去，曼哈顿的建筑方方正正地排列在一条条街道上，仿佛一个个棋子排列在键盘上。
想要计算两个建筑之间的距离，我们不能横穿某个建筑，需要拐弯抹角，经过一个个十字路口，才能到达我们想要去的地方。
曼哈顿距离另外有个名字出租车距离（cab driver distance）
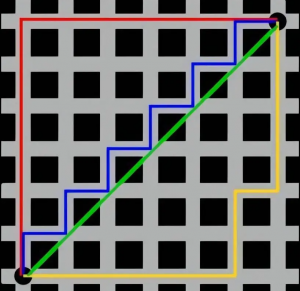
图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。
二维平面上的曼哈顿距离
假设 二维平面 内有两点：
则二维平面的曼哈顿距离公式为：
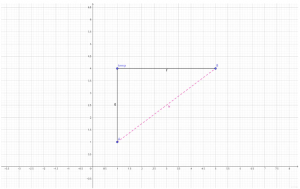
例如上图的 A(1, 1) 与 B(5, 4) , 则 AB：
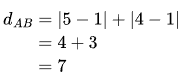
从示例可以看出：曼哈顿距离可以看成是只能上下左右(↓↑←→)走动的棋子，从A移动到B时所花费的距离。
三维空间上的曼哈顿距离
假设 三维空间 内有两点：
则三维空间的距离公式为：
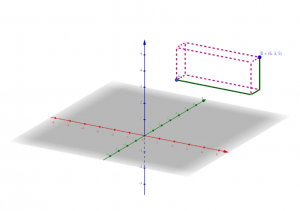
举个例子，比如上图的 A(1, 2, 3) 与 B(6, 3, 5) 两点，计算 AB:
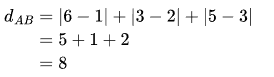
n维空间上的曼哈顿距离
假设 n维空间 内有两点：
则n维空间的距离公式为：
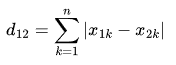（∑求和运算）