负数在计算机中,以其补码的形式表示。
原码
英文为sign-magnitude,大意应该为符号-数值的组合。
在原码中,第一个数字代表符号位,1代表负数,0代表正数,余下的为数值位,用来表示具体的数值。
5用4位二进制原码来表示就是0101
-5用4位二进制原码来表示就是1101
CSAPP中给出的原码数学公式为:
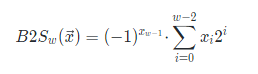
由此我们能推断出SMAXw=2w-1-1,SMINw=-(2w-1-1)。
如八位二进制原码的范围应该为[-127,127]。
反码
英文为ones’complement
一个数字用原码表示是容易理解的,但是需要单独一个位来表示符号位,并且在进行加法时,计算机需要先识别某个二进制原码是正数还是负数,识别出来之后再进行相应的运算。
这样效率不高,能不能让计算机在进行运算时不用去管符号位,也就是让符号位参与运算呢?
要实现这个功能,我们就要用到反码。
反码是一种在计算机中数的机器码表示。对于单个数值(二进制的 0 和 1)而言,对其进行取反操作就是将 0 变为 1,1 变为 0。正数的反码和原码一样,负数的反码就是在原码的基础上符号位保持不变,其他位取反。
| 十进制 | 原码 | 反码 |
|---|---|---|
| 6 | 0000 0110 | 0000 0110 |
| -3 | 1000 0011 | 1111 1100 |
下面我们来看一下,用反码直接运算会是什么情况:
step 1:我们以 6 - 3 为例,6 - 3 等价于 6 + (-3)。
6 - 3 ==> 6 + (-3) 0000 0110 // 6(反码) + 1111 1100 // -3(反码) ---------------------- 0000 0010 // (反码) 0000 0010 // 2(原码)
很明显通过反码进行 6 + (-3) 加法运算时,输出值比预期值差了一个 1。
step 2:接着我们再来看下 1 + (-1) 的运算结果:
1 - 1 ==> 1 + (-1) 0000 0001 // 1(反码) + 1111 1110 // -1(反码) ---------------------- 1111 1111 // (反码) 1000 0000 // -0(原码)
由上可知 1 + (-1) 的运算结果为 -0,而我们预期的值是 +0。
step 3:我们继续看个示例 0 + 0:
0 + 0 ==> 0 + 0 0000 0000 // 0(反码) + 0000 0000 // 0(反码) ---------------------- 0000 0000 // (反码) 0000 0000 // 0(原码)
这里我们可以知道 -0 对应的原码是 1000 0000,而 +0 对应的原码是 0000 0000。虽然 -0 和 +0 代表的数值是一样的,但是在用原码和反码表示时它们是不同的。
通过以上的多个示例,我们发现使用反码进行加法运算并不能保证得出正确的结果。
原因是用一个字节表示数字的取值范围时,这些数字中多了一个 -0。
为了解决反码出现的问题,就出现了补码。
补码
正数和 0 的补码就是该数字本身。负数的补码则是将其对应正数按位取反再加 1。
补码系统的 0 就只有一个表示方式,这和反码系统不同(在反码系统中,0 有两种表示方式),因此在判断数字是否为 0 时,只要比较一次即可。下图是一些 8 位补码系统的整数,它可表示的范围包括 -128 到 127,总共 256 个整数。
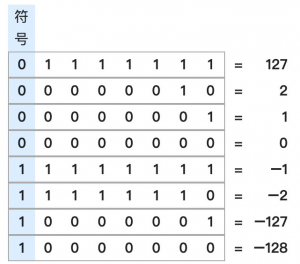
step 1:我们继续以 6 + (-3) 为例,来验证一下这个结论。
| 十进制 | 原码 | 反码 | 补码 |
|---|---|---|---|
| 6 | 0000 0110 | 0000 0110 | 0000 0110 |
| -3 | 1000 0011 | 1111 1100 | 1111 1101 |
6 + (-3) 以补码形式的计算过程如下:
6 - 3 ==> 6 + (-3) 0000 0110 // 6(补码) + 1111 1101 // -3(补码) ---------------------- 0000 0011 // 3(补码)
很明显这时我们得到了正确的结果
step 2:我们再来看一下以补码形式计算 1 - 1 的计算过程:
1 - 1 ==> 1 + (-1) 0000 0001 // 1(补码) + 1111 1111 // -1(补码) ---------------------- 0000 0000 // 0(补码)
可以发现,补码完美解决了反码的问题。
补码思想的另一种推断
时钟中,8+2=10 和 8-10=10 最终的值都是一样的。
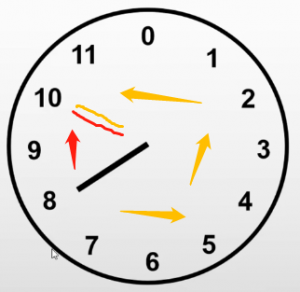
为了与二进制思想一致,这里把时钟改成了从0点开始。
8+2:从8点开始,顺时针增加2点
8-10:从8点开始,逆时针减少10点
由于 8+2 和 8-10 最终的值都是一样的,这样就可以将减法转为加法。
那么2与-10之间如何联系在一起的呢?
加法值 = 模 – 减法值
减法值 = 模 – 加法值
如果想知道8+2,模=12,加法值=2,减法值 = 12-2=10
计算101-010:
模=2³=1000
101-010 = 101+(1000-010) = 1011
模
“模”是指一个计量系统的计数范围。
时钟的计量范围是1~12,模=12。
n位的计算机计量范围是0~2^(n) -1,模=2^(n)。
“模”实质上是计量器产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。任何有模的计量器,均可化减法为加法运算。