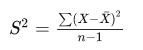方差是衡量一组变量离散程度的度量，方差越大波动越大，方差越小，波动越小。
方差计算公式
推导过程
我们知道在波动的比较厉害的数据里，每个数 跟 平均数 一般差的比较多
设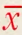
为平均数，如果我们将每个数与平均数作差，是否就能衡量波动程度呢？
例1：
7, 7, 8, 9, 9
= (7+7+8+9+9)/5 = 8
(7-8)+(7-8)+(8-8)+(9-8)+(9-8) = -1+-1+0+1+1 = 0
为什么会这样呢？
(7-8)+(7-8)+(8-8)+(9-8)+(9-8)
相当于: 7+7+8+9+9 -8 -8 -8 -8 -8
相当于: 数据之和 – 数据之和 = 0
如何解决？
在相加之前，先把每个查分别平方，去除-号
负负正正 –(平方)–> 正正正正
(7-8)²+(7-8)²+(8-8)²+(9-8)²+(9-8)²
=(-1)² + (-1)² + 0² + 1² + 1²
=1+1+0+1+1
=4
例2：
6, 7, 7, 10, 10
= (6+7+7+10+10)/5 = 8
(6-8)+(7-8)+(7-8)+(10-8)+(10-8) = -2+-1+-1+2+2
(6-8)²+(7-8)²+(7-8)²+(10-8)²+(10-8)²
=(-2)²+(-1)²+1²+2²+2²
=4+1+1+4+4
=14
从上述计算可以看出，平方和越大，数据波动性越大
例3：
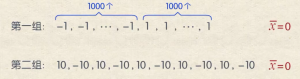
第一组数据由1000个-1与1000个1组成，=0；
第二组数据由5个-10与5个10组成，=0。
第一组平方和= 2000个1相加 = 2000；
第二组平方和= 1o个100相加 = 1000。
波动程度： 第一组 < 第二组
平方和： 第一组 > 第二组
可以看出，数据的多少影响了平方和的比较。
只要数据量足够大，即使波动程度很小，也能盖过波动更剧烈的数据。
我们用 “差距平方和/数据个数”：
第一组：2000/2000 = 1
第二组：1000/10 = 100
这次，波动程度与结果对应起来了
因此，如果我们要计算n个数的波动程度，可以进行以下操作
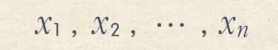
1.求平均数
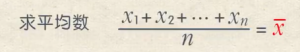
2.与平均数作差
3.求差的平方和
4.除以数据的个数
这就是“方差”的计算公式。
例1：7, 7, 8, 9, 9 = ((7-8)²+(7-8)²+(8-8)²+(9-8)²+(9-8)²)/5 = 0.8
例2：6, 7, 7, 10, 10 = ((6-8)²+(7-8)²+(7-8)²+(10-8)²+(10-8)²)/5 = 2.8
波动程度： 例1 < 例2
方差： 例1 < 例2
方差实战
例4：
根据张三、李四 5次考试成绩，查看谁更稳定？
张三：59, 61, 57, 58, 65
李四：64, 58, 62, 缺考, 56
张三：
平均数: (59+ 61+ 57+ 58+ 65)/5 = 60
方差: (-1)²+1²+(-3)²+(-2)²+5² = 40/5 = 8
李四：
平均数: (64+ 58+ 62+ 0 + 56)/5 = 60
方差: 4²+(-2)²+2²+(-4)² = 40/4 = 10
谁更稳定、谁更整齐、比较偏科 -> 都可以使用“方差”解决
方差大 -> 偏科、不稳定、不整齐
为什么不用绝对值来计算方差？
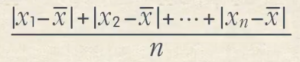
运算性质不好、不可导、二阶矩一阶矩问题
方差公式优化
1.求平均数
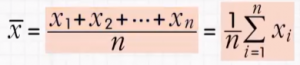
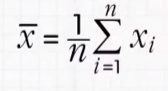
2.与平均数作差
3.求差的平方和
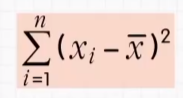
4.除以数据的个数
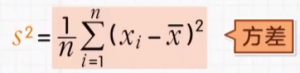
求和符号只对蓝色区域有作用
不需要知道每个数据，已知平方和和平均数，就能算出方差
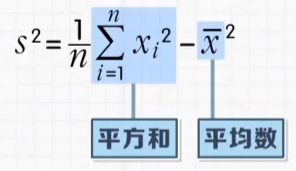
公式证明:
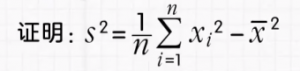
将左侧的求和公式A展开，可以转化成以下求和公式C：
将转化成的求和公式C乘上 1/n
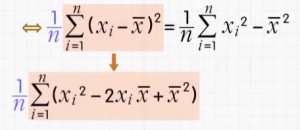
继续转换成求和公式D：
求和公式D的具体推导公式：
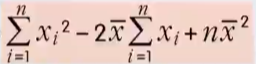
将求和公式C展开
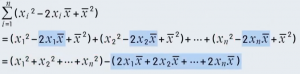
将展开后的每一项再次整理成求和公式：
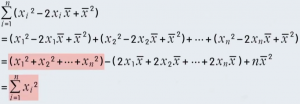
提取公因式：
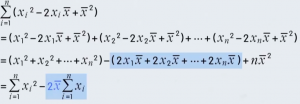
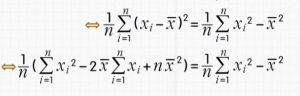
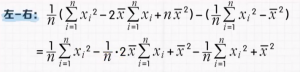
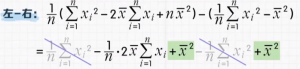
