一、一维:描述性统计
描述性统计量分为:集中趋势、离散程度(离中趋势)和分布形态。
1.1 集中趋势
数据的集中趋势,用于度量数据分布的中心位置。直观地说,测量一个属性值的大部分落在何处。描述数据集中趋势的统计量是:平均值、中位数、众数。
- 平均值(Mean):指一组数据的算术平均数,描述一组数据的平均水平,是集中趋势中波动最小、最可靠的指标,但是均值容易受到极端值(极小值或极大值)的影响。
- 中位数(Median):指当一组数据按照顺序排列后,位于中间位置的数,不受极端值的影响,对于定序型变量,中位数是最适合的表征集中趋势的指标。
- 众数(Mode):指一组数据中出现次数最多的观测值,不受极端值的影响,常用于描述定性数据的集中趋势。
1.2 离散程度
数据的离散趋势,用于描述数据的分散程度,描述离散趋势的统计量是:极差、四分位数极差(IQR)、标准差、离散系数。
- 极差(Range):又称全距,记作
,是一组数据中的最大观测值和最小观测值之差。一般情况下,极差越大,离散程度越大,其值容易受到极端值的影响。
- 四分位数极差(Inter-Quartile Range, IQR):又称内距,是上四分位数和下四分位数的差值,给出数据的中间一半所覆盖的范围。
是统计分散程度的一个度量,分散程度通过需要借助箱线图(Box Plot)来观察。通常把小于
或者大于
的数据点视作离群点。
- 方差(Variance):方差和标准差是度量数据离散程度时,最重要、最常用的指标。方差,是每个数据值与全体数据值的平均数之差的平方值的平均数,常用
表示。
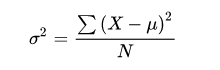
- 标准差(Standard Deviation):又称均方差,常用
表示,是方差的算术平方根。计算所有数值相对均值的偏离量,反映数据在均值附近的波动程度,比方差更方便直观。
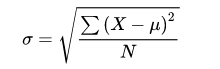
- 离散系数(Coefficient of Variation):又称变异系数,为标准差
与平均值
之比,用于比较不同样本数据的离散程度。离散系数大,说明数据的离散程度大;离散系数小,说明数据的离散程度也小。
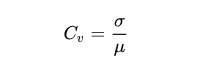
1.3 分布形态
偏度(Skewness):用来评估一组数据分布呈现的对称程度。
- 当 偏度系数
时,分布是对称的
- 当 偏度系数
时,分布呈正偏态(右偏)
- 当 偏度系数
时,分布呈负偏态(左偏)
峰度(Kurtosis):用来评估一组数据的分布形状的高低程度的指标。
- 当 峰度系数
时,是正态分布
- 当 峰度系数
时,分布形态陡峭,数据分布更集中
- 当 峰度系数
时,分布形态平缓,数据分布更分散
其他数据分布图——分位数是观察数据分布的最简单有效的方法,但分位数只能用于观察单一属性的数据分布。散点图可以用来观察双变量的数据分布,聚类可以用来观察更多变量的数据分布。通过观察数据的分布,采用合理的指标,使数据的分析更全面,避免得出像平均工资这类偏离事实的的分析结果。
1111