平均变化率
例1：在吹气球的过程中，随着气球内空气容量的变化，气球半径的增加速度越来越慢。
如何从数学角度描述这种现象呢？
将气球理想化为标准的球体，球的体积公式为：
如果将半径 r 表示为体积 V 的函数，那么r(V)可以标识为：
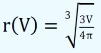
当空气容积由 k 变到 (k+1) L 时，气球的平均膨胀率为：
k 到 (k+1) 的半径差 ÷ k 到 (k+1) 的体积差
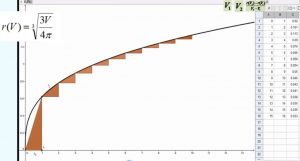
可以看出，随着气球容积的变化，气球的平均膨胀率变小了。
当空气容量从V1增加到V2，气球的平均膨胀率为：
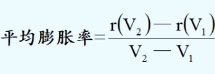
例2：
假设下面是一座山的剖面示意图，建立如图所示的平面直角坐标系，A是出发点，H是山顶，爬山路线用函数 y=f(x) 表示。
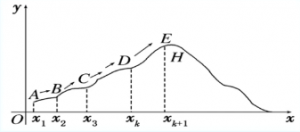
自变量 x 表示某旅游者的水平位置，函数值 y=f(x) 表示此时旅游者所在高度。设点 A 的坐标为(x1, y1)，点B的坐标为(x2, y2).
问题1. 若旅游者从点A爬到点B，且这段山路是平直的，自变量x 和函数值 y的改变量 Δx, Δy 分别是多少？
自变量x 的改变量 Δx = x2 – x1
自变量y 的改变量 Δy = y2 – y1
问题2. 能都根据Δy 的大小判断山路OE的陡峭程度？
标识A,B两点所在直线的斜率。“线段”所在直线的斜率越大，山路越陡。
因此，对于山坡AB来说，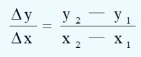
可以近似地刻画。
但是并不代表山坡OE。
函数的平均变化率
对于函数 y=f(x)，给定自变量的两个值 x1 和 x2，当自变量x 从 x1 变为 x2 时，函数值从 f(x1) 变为 f(x2).
我们把式子
称为函数 y=f(x) 从 x1 到 x2 的平均变化率。
习惯上用Δx 表示 x2 – x1，即Δx = x2 – x1，可以用 x1+Δx 代替 x2；类似的 Δy = f(x1) – f(x2)。
于是平均变化率可表示为：
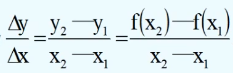
对Δx ，Δy 的理解
x1, x2 是定义域内不同的两点，因此 Δx != 0，但 Δx 可正可负，因此平均变化率可正、可负，也可为零。
导数
例3：
在高台跳水运动过程中，运动员相对于水面的高度h（单位:m）与起跳后的时间t（单位:s）存在函数关系 h(t) = -4.9t²+6.5t+10
1）求0-0.5时刻的平均速度？
2）求1-2时刻的平均速度？
问题1: 用平均速度描述运动员的运动状态有什么问题?
答:平均速度不能准确反映运动员在每个时刻的运动状态，因为运动员在每个时刻的瞬时运动状态可能是不一样的，所以很有必要找到一个能反映出运动员在每个时刻(每个瞬间)的运动状态的量，这个量可以是瞬时速度。
3）能否求出运动员在t= 2时刻的瞬间(瞬时)速度?
如果把时间段 Δt 缩小，再缩小，这样这个时间段Δt 就会向一个瞬间变化，也就是 Δt趋向于0，记作：
这样一段时间内的平均速度
就会慢慢变成在一个非常短的时间段内的平均速度，而当这个时间段再进一步趋向于0，向一个瞬间变化的时候，也就是时，就会变成瞬时。
当 Δt>0时，t2 > t1, 时间段是[t1, t2]即[2, 2+Δt]，现在我们开始不断缩小这个时间段，也就是使 2+Δt 时刻无限靠近2时刻，即At- >0：
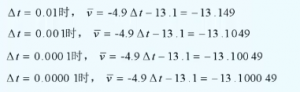
综上,我们可以看到在Δt→0的过程中，平均速度是不断的在变的，但是始终趋向于-13.1.
从物理学的角度我们知道当Δt→0时，Δt就慢慢趋向于瞬间，平均速度n在这个过程中就会慢慢向一个瞬时速度转化与靠近。所以那个平均速度靠近与趋向的数就是瞬时速度。
所以-13.1其实就是运动员在t=2时刻 瞬间速度.
用 lim 表达极限，在 t=2 时刻的瞬时速度
在t=2时刻的瞬时速度是一个时间段趋向于0时平均速度的极限值，我们也把这个极限值叫做运动员在空中相对于水面的高度h关于时间t在t=2时刻的瞬时变化率(速度)，这个瞬时速度其实就是生活中的导数值.
生活中的导数是用来描述瞬时变化的.
引申:能否求出运动员在t=1时刻的瞬间(瞬时)速度?
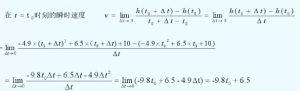
把一段时间内的平均速度向某个时刻的瞬时速度进行转化，推广
到数学里面，就是对一般函数 y= f(x) , 把 y 相对于 x 的某段变化的平均变化率转化到某个 x=x0 时的瞬时变化率。
然后使 x2 无限靠近 x1，即 x0 + Δx 无限靠近 x0, 也就是 Δx无限趋近于0,得到在 x0 处的瞬间变化率
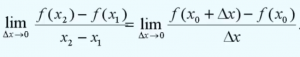
对于函数 y=f(x)，在 x = x0 处，y 相对于 x 的瞬间变化率是 
，也称这个值是函数 y=f(x) 在 x=x0 处的导数(值)。
记作：
